虽然本章主要关注二进制整数表示，但程序员通常也需要存储实数。存储实数本质上是困难的，并且没有任何二进制编码能够以完美的精度表示实值。也就是说，对于实数的任何二进制编码，都存在无法 精确 表示的值。像 pi 这样的无理值显然无法精确表示，因为它们的表示永远不会终止。给定固定的位数，二进制编码仍然无法表示其范围内的一些有理值。

与可数无限的整数不同，实数集是不可数。换句话说，即使对于较小范围的实际值（例如，0 到 1 之间），该范围内的值集合也很大，以至于我们甚至无法开始枚举它们。因此，实数编码通常仅存储已被截断为预定位数的值的近似值。如果有足够的位，近似值对于大多数用途来说通常足够精确，但在编写不能容忍舍入的应用程序时要小心。

本节的其余部分简要介绍了两种用二进制表示实数的方法：定点，它扩展了二进制整数格式，以及 浮点，它以一些额外的复杂性为代价表示大范围的值。

4.8.1. 定点数(Fixed-Point)表示

在定点表示中，值的 二进制点 的位置保持固定且无法更改。就像十进制数中的小数点一样，二进制小数点表示数字的小数部分开始的位置。定点编码规则类似于无符号整数表示形式，但有一个主要例外：二进制小数点后面的数字表示 2 的负数幂。例如，考虑八位序列 0b000101.10，其中前六位代表整数，其余两位代表小数部分。 图 1 标记了数字位置及其各自的解释。 From high-order to low-order, the digits are labeled d5, d4, d3, d2, d1, d0, d-1, d-2. d-1 contributes 0.5, and d-2 contributes 0.25 to the value.

图 1. 固定二进制小数点后两位的八位数字中每位数字的值

应用将 0b000101.10 转换为十进制的公式显示：

(0 × 25) + (0 × 24) + (0 × 23) + (1 × 22) + (0 × 21) + (1 × 20) + (1 × 2-1) + (0 × 2-2)     =    0 + 0 + 0 + 4 + 0 + 1 + 0.5 + 0    =    5.5

更一般地，在二进制小数点后的两位中，数字的小数部分保存四个序列之一：00 (.00)、01 (.25)、10 (.50) 或 11 (.75)。因此，两个小数位允许定点数表示精确到 0.25 (2-2) 的小数值。添加第三位可将精度提高到 0.125 (2-3)，并且该模式类似地继续，二进制小数点后的 N 位可实现 2-N精度。

由于二进制小数点之后的位数保持固定，因此某些具有完全精确操作数的计算可能会产生需要截断（舍入）的结果。考虑与上一个示例相同的八位定点编码。它精确地表示 0.75 (0b000000.11) 和 2 (0b000010.00)。然而，它不能精确地表示 0.75 除以 2 的结果：计算应该产生 0.375，但存储它需要二进制小数点后的第三位 (0b000000.011)。截断最右边的 1 可使结果符合指定的格式，但会产生 0.75 / 2 = 0.25 的舍入结果。在此示例中，由于涉及的位数较少，舍入非常严重，但即使更长的位序列在某些点也需要截断。

更糟糕的是，舍入误差在中间计算过程中会复合，并且在某些情况下，一系列计算的结果可能会根据计算的执行顺序而变化。例如，考虑前面描述的相同八位定点编码下的两个算术序列：

  1. (0.75 / 2) * 3    =    0.75
  2. (0.75 * 3) / 2    =    1.00

请注意，两者之间的唯一区别是乘法和除法运算的顺序。如果不需要舍入，则两次计算应产生相同的结果 (1.125)。然而，由于截断发生在算术中的不同位置，它们产生不同的结果：

  1. 从左到右，中间结果 (0.75 / 2) 四舍五入为 0.25，最终乘以 3 得到 0.75。
  2. 从左到右，中间计算 (0.75 * 3) 精确地产生 2.25，无需任何舍入。将 2.25 除以 2 轮，最终结果为 1。

在此示例中，只需为 2-3 位添加一位即可使该示例以全精度成功，但我们选择的定点位置仅允许二进制小数点后的两位。一直以来，操作数的高位都完全未使用（数字 d2 到 d5 从未设置为 1）。以额外的复杂性为代价，另一种表示形式（浮点）允许整个位范围对一个值做出贡献，而不管整数部分和小数部分之间的划分如何。

4.8.2. 浮点数(Floating-Point)表示

在浮点数表示中，值的二进制小数点 不 固定在预定义的位置。也就是说，二进制序列的解释必须对其如何表示值的整数部分和小数部分之间的分割进行编码。虽然二进制小数点的位置可以通过多种可能的方式进行编码，但本节仅关注其中一种，即电气和电子工程师协会 (IEEE) 标准 754。几乎所有现代硬件都遵循 IEEE 754 标准来表示浮点值。

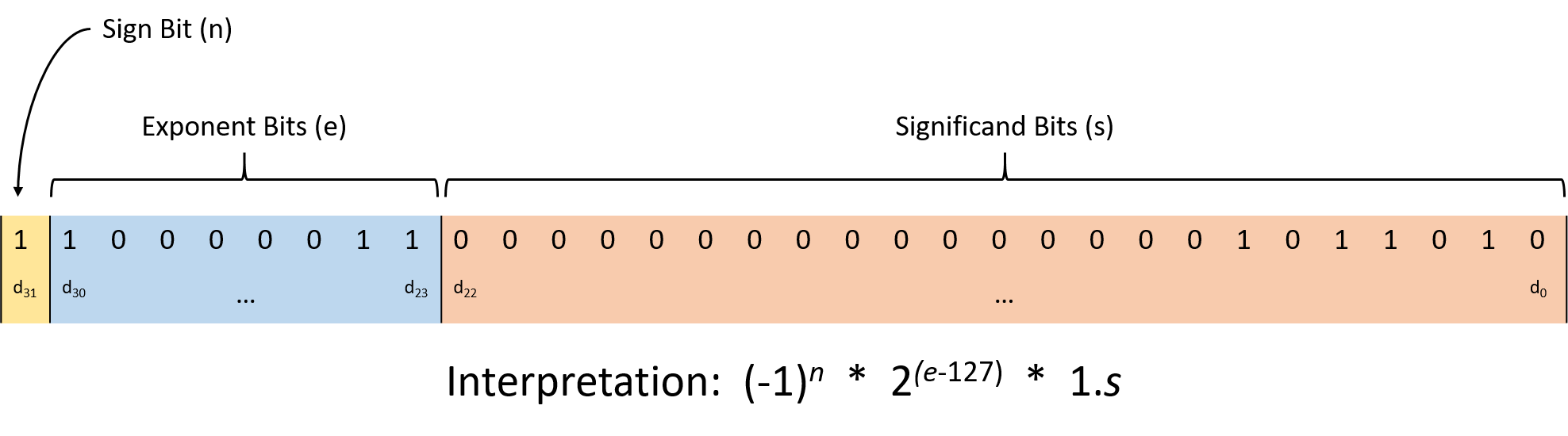
The leftmost digit represents the sign bit. The next eight bits represent the exponent, and the remaining 23 bits represent the significand.

图 2. 32 位 IEEE 754 浮点标准

图 2 说明了 32 位浮点数（C 的“float”类型）的 IEEE 754 解释。该标准将位划分为三个区域：

  1. 低 23 位（数字 d22 到 d0）表示 有效数（有时称为 尾数）。作为最大的位区域，有效数充当值的基础，最终通过与其他位区域相乘来改变值。解释有效数时，其值隐式跟随 1 和二进制小数点。小数部分的行为类似于上一节中描述的定点表示。

    例如，如果尾数位包含 0b110000…​0000，则第一位代表 0.5 (1 × 2-1)，第二位代表 0.25 (1 × 2-2)，其余位全部为零，因此不会影响该值。因此，有效数贡献 1.(0.5 + 0.25) 或 1.75。

  2. 接下来的八位（数字 d30 到 d23）表示 指数(exponent) ，它缩放尾数的值以提供较宽的可表示范围。尾数乘以 2exponent-127，其中 127 是一个 偏差(bias) ，使浮点数能够表示非常大和非常小的值。

  3. 最后的高位（数字 d31）代表 符号位，它对值是正 (0) 还是负 (1) 进行编码。

例如，考虑解码比特序列 0b11000001101101000000000000000000。有效数字部分为 01101000000000000000000，表示 2-2+ 2-3 + 2-5 = 0.40625，因此有效数字区域贡献 1.40625。指数为 10000011，代表十进制值 131，因此指数贡献的因子为 2(131-127)(16)。最后，符号位为1，因此该序列代表负值。将它们放在一起，位序列表示：

1.40625 × 16 × -1 = -22.5

虽然 IEEE 浮点标准显然比前面描述的定点方案更复杂，但它为表示各种值提供了额外的灵活性。尽管具有灵活性，但具有恒定位数的浮点格式仍然无法精确表示每个可能的值。也就是说，与定点一样，舍入问题同样会影响浮点编码。

4.8.3. 四舍五入的影响

虽然舍入不太可能破坏您编写的大多数程序，但实数舍入错误偶尔会导致一些引人注目的系统故障。 1991 年海湾战争期间，舍入错误导致美国爱国者导弹电池未能拦截伊拉克导弹。导弹造成 28 名士兵死亡，多人受伤。 1996 年，欧洲航天局首次发射阿丽亚娜 5 号火箭起飞后 39 秒爆炸。该火箭借用了阿丽亚娜 4 号的大部分代码，在尝试将浮点值转换为整数值时触发了溢出。